Il criterio del quadrato è un metodo molto semplice per determinare se un Re è in grado di intercettare un Pedone che sta viaggiando speditamente verso la promozione. Osserviamo la seguente figura: Diagramma n.1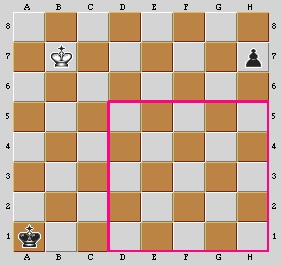 Il Re bianco riesce a fermare il Pedone?Supponiamo che sia il Bianco a dover muovere. La prossima mossa del Nero potrebbe essere 1 ..., h5, che è quella che avvicina più velocemente il Pedone alla casa di promozione. Supponendo che il Nero si limiti a muovere solo il suo Pedone, il Bianco riuscirà ad intercettarlo? È possibile determinarlo senza effettuare il calcolo preciso di tutte le varianti? La risposta è positiva, basta applicare il sottostante criterio:
Pertanto il Bianco, se vuole riuscire ad intercettare il Pedone e neutralizzare la promozione, deve assolutamente entrare in tale quadrato: 1 Rc6! (l'unica mossa esatta), h5; 2 Rd5 (il Re bianco è entrato nel quadrato), h4; 3 Re4, h3; 4 Rf3, h2; 5 Rg2, h1=D+; 6 R:h1 e il Bianco pareggia per patta teorica. Ma il criterio del quadrato afferma che la regola è valida se non ci sono altri ostacoli. Cosa succede dunque se il Nero decide di usare il Re invece di spingere sempre e solo il Pedone? Ebbene, nella posizione del diagramma n.1 il Re nero è troppo distante dal suo Pedone per poter costituire un ostacolo al Re bianco. Ecco un esempio: 1 Rc6!, Rb2; 2 Rd5, Rc3; 3 Re5, h5; 4 Rf4, h4; 5 Rg4, h3; 6 R:h3 e patta. Se al contrario nella posizione del diagramma n.1 fosse il Nero a dover muovere prima, allora il Bianco sarebbe spacciato perché il suo Re non avrebbe alcuna possibilità, a gioco corretto, di entrare nel quadrato del Pedone e quindi non sarebbe in grado di neutralizzarne la promozione: 1 ..., h5!; 2 Rc6 (inizio di un inseguimento disperato ed inutile), h4; 3 Rd5, h3; 4 Re4, h2; 5 Rf3, h1=D+ ed il Nero vince. Indice |
| 
|
Autore: Andreas Vogt ® 1998